SCUBA DIVING EXPLAINED Questions and Answers on
Lawrence Martin, M.D. Copyright 1997
|
|||||||||||||||||||
|
Home Brief History of Diving Glossary
|
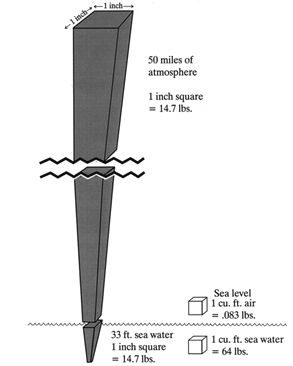
SECTION EWater and the Physical Laws That Affect All DiversWHAT ARE THE IMPORTANT DIFFERENCES BETWEEN AIR AND WATER? The gas laws discussed in Section D apply equally well to air at any pressure. The laws are particularly important in understanding what happens to air-containing spaces under water, particularly the lungs, sinuses, and middle ears. Before discussing air pressure under water, it will be useful to review important differences between air and water (Table 1). 1) Water is much heavier than air. A cubic foot of air weighs 1/12 pound (lb). A cubic foot of fresh water weighs 62.4 lbs and a cubic foot of sea water weighs 64 lbs. (Figure 1). 2) Water molecules are made up of hydrogen and oxygen, chemical symbol H2O. Each water molecule contains two atoms of hydrogen and one atom of oxygen. Salt water contains salt (sodium chloride, chemical symbol NaCl) and other minerals in solution (i.e., dissolved into it, not chemically combined with the water). Salt adds to the weight of water, and for this reason sea water has slightly greater weight - and hence pressure - than fresh water (sea water contains approximately 35 pounds of salt for every 1000 pounds of water). It takes a depth of 34 feet of fresh water to equal one atmosphere of pressure, as opposed to 33 feet of sea water. 3) Air is a mixture of gases, principally oxygen (O2, 21% of the air by volume) and nitrogen (N2, 78% by volume). Each gas exerts its own independent pressure, the sum of which equals the total air pressure (Dalton's law). Unlike water, air (and any other gas or mixture of gases) is compressible; the greater the pressure exerted, the more tightly packed together are the individual gas molecules. Regardless of the air pressure, however, water molecules are much more tightly packed together than air molecules. Compared to air at sea level pressure (1 atm.), water is about 800 times denser. 4) Just as air has weight and exerts pressure on all sides of an object in the atmosphere, water exerts pressure around any object immersed in it. We can push water out of the way because its weight is distributed on all sides and the molecules can be easily moved. The resistance we feel under water reflects the extreme density of water (compared to air), and the fact that it takes time for water molecules to move out of the way. 5) Water pressure, like air pressure, is a function of weight; the deeper one goes the greater the surrounding water pressure. The marked increase in water pressure with depth affects every scuba and non-scuba diver, indeed anyone who goes under water (unless inside a heavy vessel with walls that resist pressure, such as a submarine).
Figure 1. Weight of water vs. air at sea level.
6) Since water is not compressible, unlike air it does not become denser as pressure increases. A cubic foot of water at 130 feet depth has the same weight and density as a cubic foot of water at 33 feet. In contrast, a cubic foot of air at sea level weighs more than a cubic foot of air in the Rocky Mountains or the Himalayas. 7) Differences between air and water, in both weight and density, predict a radical difference in pressure with changes in altitude/depth. Sea water pressure changes one whole atmosphere every 33 feet (every 34 feet for fresh water). Provided they are of the same circumference, a column of sea water 33 feet high weighs the same as a column of earth's entire atmosphere. 8) Water freezes, whereas air does not freeze at any temperature occurring in nature. Sea water freezes at a much lower temperature than fresh water because of the dissolved salt, which slows down the formation of water crystals.
TEST YOUR UNDERSTANDING Answers WHAT DOES BOYLE'S LAW PREDICT ABOUT CHANGES IN PRESSURE WITH DEPTH? It is always convenient to illustrate Boyle's law with balloon models. Balloons are round and easily compressible. By taking an air-filled balloon under water, Boyle's law can be nicely demonstrated (Figure 2). Assume a balloon is filled with 12 liters of air at the surface, then taken under water. Figure 2 shows the changes in density and air volume with depth as predicted by Boyle's law. The balloon shrinks and its air becomes denser with increasing depth; this is because the pressure increases with depth and the balloon is compressible. On ascent the opposite happens; the balloon re-expands and the air density returns to baseline.
TEST YOUR UNDERSTANDING Answers
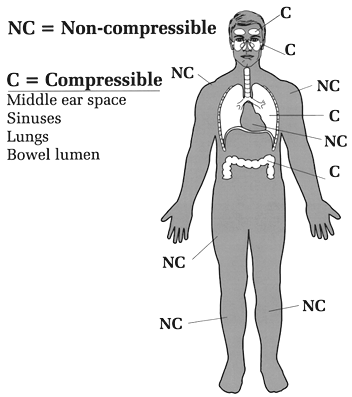
So much for balloons. What about the body? Underwater, we can view the body as made up of two groups of organs that differ in how they respond to water pressure. One group of organs is compressible by the water pressure, and the other group is non-compressible (Figure 3). Bone, muscle, blood and solid organs such as the kidney, heart, and liver are all non-compressible and therefore unaffected by water pressure; these organs and tissues have the same (or higher) density than water and can withstand intense water pressure without any problem. Were our bodies made up of only non-compressible structures, going under water would be a lot simpler (though still not hazard-free). The compressible areas contain some air and include the lungs, middle ears, sinuses, nasal passages, interior of hollow organs (stomach and intestines), and any air pockets you may not know about (e.g., a tooth cavity). If these parts of the body did not contain air they would not be compressible. Conversely, any part of the body that is compressible under water must contain air or some other gas. At the moment a diver holds his breath the mass of air in the body is fixed; no new air can enter or leave. Given that the mass of air is fixed at that point, Boyle's law predicts that the compressible spaces will be affected by changes in pressure. A fixed mass of gas (the diver's air-containing spaces) subjected to an increase in pressure underwater will compress (shrink in size). But by how much? Assume a typical breath-hold diver's lungs contain 8 liters of air at full inhalation (one liter equals about one quart). At 33 feet his lungs could theoretically shrink to half the sea level volume, or 4 liters, if they behave just like a balloon. The same percent shrinkage could occur in the sinuses, middle ears, and all other compressible body spaces, if they too behave like balloons. However, our air-containing spaces don't behave exactly like balloons; they are not as easily and evenly compressible. The lungs are supported by a bony rib cage, the sinuses are embedded in the skull, only part of the middle ear is exposed to water pressure (the tympanic membrane), etc. Also, trained breath-hold divers can transfer some air from the throat to the middle ear (via the eustachian tube), retarding the shrinkage of that small space. So, on the one hand, our compressible air spaces are much more complex than the simple balloon models used to illustrate Boyle's law. On the other hand, we do have compressible air spaces and Boyle's law predicts that they must shrink in size if the outside pressure is greater than the inside pressure. It is just impossible to predict exactly how much they will shrink, or how such shrinkage will affect the individual diver. If the breath-hold diver goes too deep, the spaces will shrink so much that blood starts leaving the capillaries to fill in the spaces. The result can be lung, sinus or nasal hemorrhage, or a ruptured tympanic membrane. With ascent, all the breath-hold diver's shrunken spaces will expand back to their original size. Because there is no over expansion, there is no risk of blowing out a lung or other air space.
Figure 3. Compressible and non-compressible organs. Breath-hold diving, practiced for centuries, is still employed for both recreation and commerce (ama divers of Japan and Korea, pearl divers of Hawaii, resort divers of Mexico, sport divers of California). It requires special skills beyond the ability to hold one's breath, such as withstanding the squeeze of descent and quickly accomplishing a goal when the desired depth is reached. Scuba requires none of these skills but others, of a different sort, that are easy to learn. For most people, scuba is much easier to master than breath-hold diving.
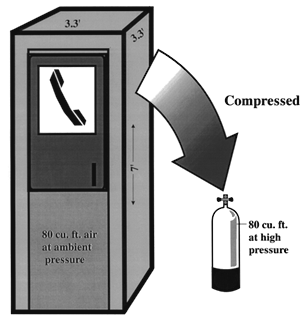
TEST YOUR UNDERSTANDING Answers WHAT DOES BOYLE'S LAW PREDICT FOR THE DIVER BREATHING COMPRESSED AIR? Water contains oxygen (both dissolved and as part of the water molecule, H2O). Unlike fish, land animals are not equipped to extract the dissolved or free oxygen and use it for breathing. Like all other mammals (including the aquatic variety such as dolphins, porpoises and whales), humans under water are cut off from life-supporting oxygen. For centuries the only underwater option was breath-hold diving, an activity practiced only by the most daring and hardy. For most people even 20 seconds under water can seem like eternity. The advent of scuba made it possible for just about anyone with healthy lungs and heart to stay under water for long periods. (This advance has not come without a price. Compressed air diving presents two physiologic problems breath-hold divers don't worry much about: decompression sickness and air embolism.) Boyle's law predicts that the compressible spaces of a breath-hold diver will compress because the amount of air in these spaces (i.e., the total number of air molecules) is fixed at the point of breath-hold; hence, as pressure increases the volume occupied by the air must decrease. Does Boyle's law also apply for scuba divers? Absolutely; after all, a law is a law. But the consequences are different because scuba divers breathe compressed air under water. First, the amount of air (the number of air molecules) in each of the scuba diver's compressible spaces increases along with the water pressure. Second, the volume of each compressible space remains fairly constant throughout the dive. Thus even though a space is compressible it should not be compressed during scuba diving. While diving, the extra molecules of air that enter these spaces (lungs, sinuses, middle ears) allows them to maintain the same pressure as the surrounding water pressure. At a given depth, though the ambient pressure is increased the volume in any compressible space remains constant because the gas density increases. Compressible body spaces while scuba diving (compared to sea level) have: Same volume (size) Increased number of gas molecules Increased gas density HOW MUCH AIR IS IN A SCUBA TANK? Scuba dives can remain under water because they carry a supply of air. The amount of air carried in a tank depends on its size and filling pressure. Most tanks used for recreational diving are designed to carry anywhere from about 60 to 100 cu. ft. of air; the typical tank found in most resorts carries 80 cubic feet (cu. ft.) when filled to 3000 psi. If the tank is filled to a lower pressure the volume of air it contains will be less. Eighty cu. ft. is the volume inside a box 5 ft. x 4 ft. x 4 ft., or the volume of a telephone booth 7 ft. x 3.3 ft. x 3.3 ft. (Figure 4). Since a cubic foot of air weighs 1/12 lb, the air in an 80 cu. ft. tank filled to capacity weighs about 6.7 lbs. This weight is in addition to the much heavier weight of the tank itself.
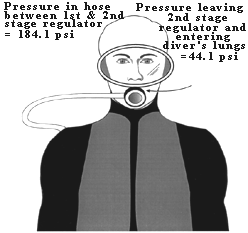
Figure 4. An 80 cu. ft. capacity scuba tank can hold as much air as would fill a telephone booth 7 ft. x 3.3 ft. x 3.3 ft. at sea level. HOW DOES AIR PRESSURE CHANGE FROM THE SCUBA TANK TO THE DIVER'S LUNGS? Sea level pressure is 14.7 psi. An 80 cu. ft. tank at 3000 psi contains 80 cu. ft. of air that has been compressed 204 times (3000 psi/14.7 psi) higher than sea level pressure. If you tried to breathe air at 3000 psi it would blow you away; you couldn't do it. The scuba diver is able to breathe tank air by virtue of a two-stage regulator system that 1) steps the pressure down to a level slightly above ambient, and then 2) delivers the air at ambient pressure. Table 3 shows examples of regulator and airway pressures for various depths. The first stage regulator brings the pressure down to ambient + a predetermined pressure. The pre-determined pressure is set by the regulator's design, but is generally 120-140 psi. Thus the pressure in the hose between first and second stages is 120 to 140 psi higher than the ambient pressure. The second stage regulator contains a demand valve that requires only a slight inspiratory effort to open; when the diver inhales on the mouthpiece attached to the second stage, the demand valve opens and air enters the lungs at ambient pressure. Note that the air is at the pre-determined pressure immediately upon leaving the second stage (i.e., 120-140 psi), but it rapidly reaches ambient by the time it is inhaled (Figure 5). The second stage regulator is also designed so that air flow ceases when the diver exhales. (When air flow doesn't cease on exhalation it is said to "free-flow," a problem that can usually be corrected by adjusting the regulator or briefly occluding the mouthpiece.)
Figure 5. Scuba diver at 66 fsw (3 atm. or 44 psi) The pressure in the hose connecting the first stage and second stage regulators is the ambient pressure + 140 psi or 184.1 psi. The air pressure leaving her second stage regulator is at ambient pressure (44 psi). The pressure in the tank (on her back, not shown) does not affect the regulator pressures (as long as the tank pressure is above some minimum value, usually the ambient pressure).
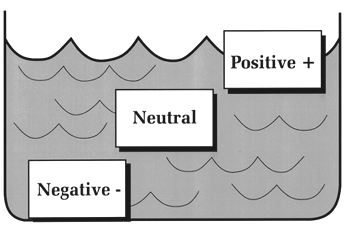
TEST YOUR UNDERSTANDING Answers WHAT IS BUOYANCY? Buoyancy refers to the tendency of objects immersed in water to float or sink. Objects that are positively buoyant float on top of water; objects that are negatively buoyant sink; and objects that are neutrally buoyant neither float nor sink, but stay where you place them (Figure 6). This principle was first stated by Archimedes (Greek mathematician and engineer, lived about 287 B.C. to 212 B.C.). He observed that an object immersed in water sinks or floats depending on the weight of water it displaces. If the weight of water displaced is less than the object's weight, it sinks; if the displaced water weighs more, the object floats; and if the displaced water is the same the object is neutrally buoyant.
Figure 6. Objects that float are positively buoyant and those that sink are negatively buoyant. Objects that stay where placed are neutrally buoyant. For example, a cubic foot of solid wood weighing 63 lbs. would float in sea water (cu. ft. = 64 lbs) and sink in fresh water (cu. ft. = 62.4 lbs.). A cubic foot of solid steel weighs much more than 64 lbs., and so will sink in any body of water, whereas a cubic foot of styrofoam will always float. The steel displaces much less than its weight of water, the styrofoam much more. WHAT IS BUOYANCY CONTROL? "Buoyancy" also refers to an all important scuba diving skill, perhaps the one most difficult to master. A diver who has learned to control buoyancy has learned: the proper amount of lead weight to carry for each dive; how to use natural breathing to inflate or deflate the lungs to control vertical position; how to position equipment in order to stay horizontal; when (and when not) to put air in the BC; and how to ascend at a slow and steady rate. Good buoyancy control is perhaps the single skill that most distinguishes experienced from novice divers. For most divers it does not come easily or quickly. Consider the many factors that can affect a diver's buoyancy: Innate buoyancy differs among individuals, and depends on the amount and distribution of body fat, bone and muscle; as a result, some people naturally float and some sink. Fat tissue has a lower density than bone or muscle, so people with a lot of fat are more likely to float (i.e., displace an amount of water weighing more than their body), whereas lean, muscular folks are more likely to sink (i.e., displace an amount of water weighing less than their body). The amount of air in the lungs affects buoyancy. If you establish neutral buoyancy during quiet breathing, a full inhalation will make you rise (become positively buoyant), whereas a full exhalation will make you sink (negatively buoyant). A wet suit will be positively buoyant on the surface but will change to neutrally or negatively buoyant at depth. A typical 80 cu. ft. aluminum scuba tank filled with air is negatively buoyant by 2-3 lbs., but when near empty the same tank will be 2-3 lbs. positively buoyant. (80 cu. ft. or air weighs about 6 lbs.) The typical buoyancy compensator is positively buoyant without any air, and becomes more so as it is inflated. Most ancillary equipment carried on a dive, such as a light, knife, or camera, tends to sink and therefore adds to negative buoyancy. Some fins are positively buoyant, some negatively buoyant. Finally, salt water weighs more than fresh water (64 lbs. vs. 62.4 lbs. per cu. ft.), so divers are more buoyant in salt than in fresh water. Because most people have slight positive buoyancy naturally, and because the BC and wet suit add to positive buoyancy on the surface, it is usually necessary to carry lead weights while diving. Weights tip the scale to negative buoyancy and allow the diver to sink easily below the surface. Depending on body makeup and type of equipment carried or worn, warm water divers need anywhere from 4 to about 12 pounds of lead weight. The single item most affecting the amount of weight required is the wetsuit (the thicker the suit, the more weight needed to establish negative buoyancy). As the dive progresses buoyancy is constantly changing. Consider: Pressure compresses air cells in the wet suit, so the positive buoyancy contributed by the suit on the surface decreases significantly at depth. As air is used up, the tank's buoyancy changes from negative to neutral to positive (steel tanks remain negative buoyant throughout the dive). Any air in the BC at depth will expand as the diver rises, increasing buoyancy steadily with ascent; the higher the diver ascends the greater the increase in positive buoyancy. Any change in the breathing pattern during the dive (e.g., a tendency to hyperventilation) may alter the diver's average lung volume, and thus affect buoyancy. For the novice diver the net result of all the factors affecting buoyancy can be confusion and a bad dive. Consider two typical scenarios. Novice A goes to 60 feet with a group of other divers. He has trouble emptying his BC of air and kicks hard to stay at depth and with the group; no matter how hard he tries to stay down he keeps rising. He looks in vain for something to hold on to. His depth gauge shows 40 feet...then 30...then 20. He simply cannot dump any air out of his BC and a few seconds later breaks through the surface of the water. Novice B claims trouble sinking on her dives. She enters the warm Caribbean water with 16 pounds of lead, even though the dive master warns "it is too much." At 50 fsw she has difficulty staying off the bottom and puts some air in her BC. She then starts to rise, so she dumps some air. All the while she notices herself kicking hard to stay level and with her buddy. About 20 minutes into the dive she alerts her buddy that her tank has only 800 psi; her buddy still has 1800 psi. Together they begin an ascent to the safety stop line. Diver A's problem was a BC with residual air that he could not properly vent. The closer he came to the surface the quicker he rose, as air in his BC expanded further. Fortunately he did not hold his breath and suffered no barotrauma from the rapid ascent. Diver B's problem was carrying too much weight; this caused her to work extra hard under water just to stay level. As a result, she used up air much faster than her buddy. As with Diver A, she had a less than optimal dive because of poor buoyancy control.
TEST YOUR UNDERSTANDING Answers WHAT CAUSES WEIGHTLESSNESS UNDER WATER? To "float" as if defying gravity - a feeling of weightlessness - is one of the many thrills of diving. The feeling comes from establishing neutral buoyancy under water. At that point the gravity force pulling your body down is equal to the water pressure pushing it up, and you neither sink nor rise. The sensation is reportedly similar to what is experienced in outer space, which is why astronauts train with scuba gear before some space missions. However the mechanisms are different. In outer space the astronaut is far enough away from earth to escape the effects of gravity, and it is gravity which makes us have (and feel) weight. On the surface or under water, gravity still exerts an effect, but it can be nullified by establishing neutral or positive buoyancy. In outer space lead weights will float just like the astronaut because they are also free of earth's gravity. When a diver is neutrally buoyant, his weight belt, if detached, will quickly drop because it is negatively buoyant and subject to earth's gravity. HOW DOES ONE LEARN TO ACQUIRE PROPER BUOYANCY? First, understand that buoyancy is not a static phenomenon, but one that changes constantly in the water, even if you stay at a level depth (because the quantity of tank air is constantly decreasing, and also because breathing affects buoyancy). Appreciating buoyancy as a constantly changing factor during every dive is the first step to mastering it. Second, understand the role of the BC. As a rule, one should not have to rely on the BC for buoyancy control. For novice divers this piece of advice may seem paradoxical; a BC is, after all, a buoyancy compensator (sometimes also referred to as a buoyancy control device). No matter. Experienced divers learn how to use their lungs to fine tune buoyancy, and reserve the BC for an occasional adjustment, mainly to compensate for the decrease in wet suit buoyancy with depth. Ideally, inflating the BC should only be necessary on the surface (for flotation), for wet suit compensation, and for emergency ascents. However, because wet suit compression will alter buoyancy at depth, it is often necessary to add a little air to compensate and re-establish neutral buoyancy. From that point of the dive, buoyancy should be controlled mainly by breathing. (It will also be necessary at the end of the dive to dump out any air added to the BC, in order to prevent too rapid an ascent.) Third, one can take a formal buoyancy control course, offered in many resorts around the world. These courses teach the nuances of buoyancy control, including how to position equipment on your body so weight is evenly distributed. Finally, gain experience. There is no substitute for experience, which means making many dives. Some divers find that learning good buoyancy control takes perhaps 100 or more dives. It also helps to practice such basic open water skills as the fin pivot. (In this skill the diver establishes neutral buoyancy with only his fins touching the bottom; using his fins as the fulcrum, he can then rise up with each deep inhalation, and fall back toward the bottom with each exhalation.) Only with many dives can one experiment with equipment, weights, wet suits and breathing techniques, and learn to master buoyancy control. Answers to TEST YOUR UNDERSTANDING 1. Both a and b are correct. A square-foot column of sea water 33 ft. deep weighs 33 ft. x 64 lbs./ft. = 2112 lbs. This is equivalent to the weight of a column of air one foot square extending from sea level to outer space. 2. c. Since air at sea level weighs only 1/12 lb. per cubic foot, it would require 64 x 12 = 768 cu. ft. of air to equal the weight of one cu. ft. of sea water. 3. No. 4. At 6 atm. (165 fsw) the balloon would be compressed to 1/6 its original volume, or 2 liters. 5. Ans. 8 liters. From 99 fsw to 33 fsw the volume will double to 4 liters; it will double again from 33 fsw to the surface. 6. Increase, as explained by Boyle's law 7. b. The new volume would be four liters if lungs behaved like balloons. Because of the bony rib cage and other anatomic features lungs don't behave exactly like balloons, so the final lung volume would be somewhat greater than four liters. 8. a. cease 9. None. The tank, usually made of steel or aluminum, is strong enough to withstand pressures much greater than those encountered while diving. Consequently, air pressure within the tank is unaffected by the ambient pressure. Once air leaves the tank and enters the lungs its pressure will be the same as ambient. 10. c. Neutrally buoyant. 11. c. Neutrally buoyant. The volume of sea water displaced has the same weight (192 lbs.) as the diver + equipment. 12. b. Negatively buoyant. The volume of fresh water displaced weighs 187.2 lbs., which is less than the weight of diver + equipment (192 lbs.), so the diver will sink. REFERENCES AND BIBLIOGRAPHY Quoted sources and general references are listed by section or sections, in alphabetical order. An asterisk indicates references that are especially recommended. Medical textbooks and journal articles can be obtained from most public libraries via inter-library loan. For a list of companies that distribute free catalogs of diving books and videos, see Section U. SECTION E. Water and the Physical Laws That Affect All Divers For the sport diver, the training manuals of NAUI, PADI and SSI provide much useful information on physics and physiology of diving, as well as on all the diving skills. In addition, the following six books are highly recommended reference works for those who wish to read further on dive physics and physiology; the last three are textbooks marketed mainly to physicians and other medical professionals. *Hornsby A, Brylske A, Shreeves K, Averill H, Seaborn C. Encyclopedia of Recreational Diving. International PADI, Inc., Santa Ana, CA.; 1989. *NOAA Diving Manual, 3rd Edition. U.S. Department of Commerce, National Oceanic and Atmospheric Administration, Washington, D.C.; 1991. *U.S. Navy Diving Manual, Vol. 1 (Air Diving) and Vol 2 (Mixed-Gas Diving), Best Publishing Co., Box 30100, Flagstaff, AZ; 1993. *Bennett P, Elliott D, editors. The Physiology and Medicine of Diving. 4th edition. W.B. Saunders Co., Philadelphia; 1993. *Bove AA, Davis JC, editors. Diving Medicine. 2nd Ed., W.B .Saunders., Philadelphia; 1990. *Edmonds C, Lowry L, Pennefather J. Diving and Subaquatic Medicine. Butterworth
Heinemann, Oxford; 1992. |